Погрешность - 1
Рассмотрим пример оптимизации процессов, где можно применить генеративную симулюцию для анализа эффекта погрешностей чтобы оценить количество бракованных деталей.
Сценарий
Допустим, что на станке 'А' производят две детали: 'х' и 'y', а из них собираетя делать 'z' размер которой должен попадать в интервал при условии что . Если деталь 'z' имеет размер:
- в интервале [39.6мм, 40.4мм] то деталь нормальная (категория: 'ok')
- менее 39.6мм то она считается бракованной (категория: 'fail')
- более 40.4мм, то ее требуется отправить на доработку (категория: 'rework')
Далее допустим что номинальные размеры деталей:
- х :
- y :
Также допустим, что из данных, собранных при изготовление предыдушей партии, вычислено, что станок 'А' производит детали с гауссовско-распределенными погрешностями:
Задача: Оценить количество деталей, которые будут отбракованы и количество деталей, которые попадут на доработки
Моделирование
Чтобы провести оценку, построим графовую модель с четырмя узлами:
- узлы x и y - непрерывные случайные (continuous) переменные с гауссовскими распределениями
- узел z с формулой (deterministic):
- узел state с формулой (deterministic) if-elif-else
- классифицирует конкретную деталь на три категории: 'ok', 'fail', 'rework':
- ок ('ok') :
- доработка ('rework') :
- брак ('fail'):
- классифицирует конкретную деталь на три категории: 'ok', 'fail', 'rework':
Используя mBayes создаем граф и запускаем симулюцию, получаем следующее визуализацию:
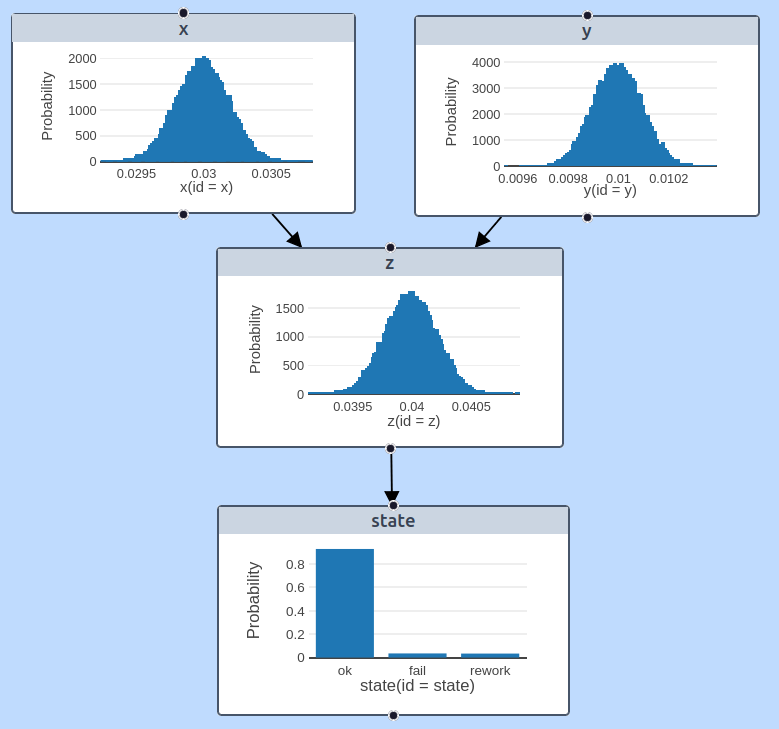
Считывая результат с гистограммы 'state' получаем следующие значения:
| state | Вероятность | Процент |
|---|---|---|
| ok | 0.927 | 92.7% |
| fail | 0.037 | 3.7% |
| rework | 0.036 | 3.6% |
Тем самым вероятности получения бракованной детали и детали, требующей доработку, равны и составляют примерно 3.6%.